|
La force de coriolis
Dans un système de référence (référentiel) en rotation uniforme, les corps en mouvement, tels que vus par un observateur partageant le même référentiel, apparaissent sujets à une force d'inertie perpendiculaire à la direction de leur mouvement. Cette force est appelée force de Coriolis en l'honneur de l'ingénieur français Gaspard-Gustave Coriolis.
Représentation mathématique
La force de Coriolis FC est perpendiculaire à l'axe de rotation du référentiel et au vecteur de la vitesse du corps en mouvement. Si le corps s'éloigne de l'axe de rotation, FC s'exerce dans le sens contraire de la rotation. Si le corps se rapproche de l'axe de rotation, FC s'exerce dans le même sens que la rotation.
Représentation vectorielle
On peut représenter FC comme un produit vectoriel en utilisant 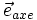 le vecteur unitaire parallèle à l'axe de rotation :
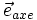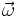On peut de plus multiplier la vitesse angulaire ω avec , ce qui produit le vecteur  . Le vecteur 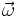décrit ainsi à la fois la direction et la vitesse  angulaire. Avec la masse m et le vecteur vitesse l'équation devient alors :
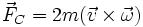
Effets
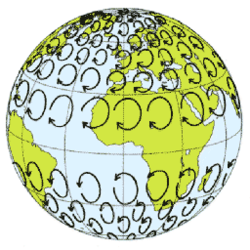
La force de Coriolis permet l'interprétation de beaucoup de phénomènes à la surface de la Terre; par exemple le mouvement des masses d'air et des cyclones, la déviation de la trajectoire des projectiles à grande portée, le changement du plan de mouvement d'un pendule tel que montré par Foucault dans son expérience du pendule de Foucault en 1851 au Panthéon, ainsi que la légère déviation vers l'est lors de la chute libre.
|
